Un ordinateur quantique étudie les nœuds mathématiques
Il est extrêmement difficile de distinguer les nœuds les uns des autres. Un nouvel algorithme quantique pourrait à l'avenir aider les mathématiciens dans cette tâche titanesque.
Pouvez-vous distinguer au premier coup d'œil une boucle de corde d'arc d'un nœud de batelier ? Non ? Vous n'êtes probablement pas le seul. Même pour les scientifiques, ce type de problème n'est pas trivial. En fait, l'une des tâches les plus importantes de la topologie est de trouver des méthodes fiables pour distinguer les différents nœuds. En effet, ces derniers ne jouent pas seulement un rôle important en mathématiques : des nœuds apparaissent également régulièrement en physique ou en biologie.
Les mathématiciens ont donc introduit ce que l'on appelle des invariants : des grandeurs caractéristiques qui diffèrent d'un nœud à l'autre. Le polynôme de Jones, introduit en 1984, s'est révélé particulièrement utile. Les nœuds identiques ont toujours le même polynôme de Jones. Le problème : pour les nœuds compliqués, il est très difficile de déterminer le polynôme correspondant - ou même de le calculer pour certaines valeurs. Mais aujourd'hui, des chercheurs dirigés par le physicien Konstantinos Meichanetzidis ont développé un algorithme quantique qui évalue efficacement les polynômes de Jones - même lorsque les ordinateurs traditionnels échouent dans leur tâche. Ils ont présenté leurs résultats dans un travail qui n'a pas encore été évalué par un comité de lecture.
Les nœuds accompagnent l'humanité depuis des millénaires. Les mathématiciens ne les étudient toutefois que depuis le 19e siècle. A cet égard, les nœuds mathématiques diffèrent légèrement de ce que l'on entend par là dans la vie quotidienne : en mathématiques, les nœuds sont toujours fermés, comme si l'on collait les extrémités d'un lacet. Pour leurs recherches, les spécialistes ont commencé à les dessiner. En fait, les nœuds sont des courbes dans un espace tridimensionnel, mais ils ont projeté les formes sur un plan, ce qui les rend plus faciles à manipuler. Mais la question s'est rapidement posée : quand deux images correspondent-elles à un seul et même nœud ?
Source : jkasd / Knoten-Tabelle
Il est encore assez facile de distinguer les nœuds simples, mais il devient difficile de garder une trace des spécimens présentant de nombreux croisements. Dans ce cas, le polynôme de Jones est utile. En fonction des croisements, il est possible d'attribuer à un nœud un polynôme qui satisfait aux propriétés suivantes : Deux nœuds identiques ont le même polynôme, tandis qu'un non-nœud a le polynôme 1.
C'est super intéressant - et un lien assez étrange entre les mathématiques et le calcul quantique
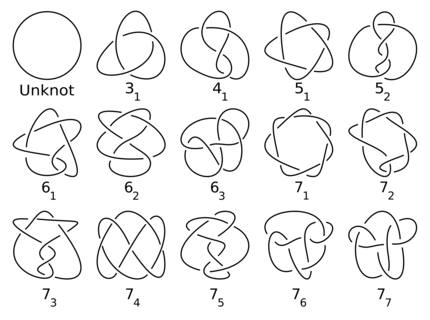
Toutefois, la définition du polynôme de Jones n'exclut pas que deux nœuds différents possèdent le même polynôme (ce qui est toutefois très rare). Néanmoins, le polynôme de Jones s'avère extrêmement utile - d'autant plus qu'il a un lien avec la physique quantique, reliant ainsi de manière inattendue la théorie des nœuds à un tout autre domaine de recherche. «C'est super intéressant - et un lien assez étrange entre les mathématiques et le calcul quantique», déclare Meichanetzidis, auteur principal de l'étude Quantinuum actuelle.
En principe, le polynôme de Jones d'un nœud peut toujours être calculé - mais la tâche devient extrêmement fastidieuse à mesure que la complexité du nœud augmente. En effet, le nombre d'étapes de calcul nécessaires pour calculer le polynôme augmente de manière exponentielle avec le nombre d'intersections d'un nœud. C'est pourquoi les ordinateurs traditionnels sont rapidement bloqués lorsque les nœuds deviennent trop compliqués. Et les ordinateurs quantiques ne sont d'aucune aide : les algorithmes quantiques connus ne peuvent malheureusement pas empêcher le nombre d'étapes de calcul d'augmenter de manière exponentielle.
En route vers un avantage quantique utile
Mais les ordinateurs quantiques offrent un autre avantage : Dès 2005, des physiciens dirigés par l'informaticienne Dorit Aharonov ont montré que les calculateurs quantiques pouvaient approcher efficacement le polynôme de Jones d'un nœud pour certaines valeurs - c'est-à-dire que le nombre d'étapes de calcul nécessaires n'augmente que de manière polynomiale avec le nombre de croisements. Les chercheurs de l'entreprise d'informatique quantique Quantinuum ont développé et mis en œuvre un tel algorithme quantique en détail. En revanche, même pour cette approximation, un ordinateur ordinaire a encore besoin d'un nombre extrêmement élevé d'étapes de calcul, dont le nombre croît de manière exponentielle avec la taille du nœud.
«Si nous évaluons notre algorithme quantique pour différentes valeurs, il est très probable qu'il permette de distinguer efficacement les nœuds les uns des autres», explique Meichanetzidis. Par exemple, si le même résultat est obtenu pour deux nœuds lors de plusieurs évaluations du polynôme de Jones, il est probable que les deux nœuds soient identiques. Cela peut être exploité dans le cadre de la théorie des nœuds, par exemple pour aborder certaines des conjectures ouvertes du domaine. Par exemple, la conjecture de Jones stipule qu'aucun nœud, à l'exception du non-nœud, n'a un polynôme de Jones égal à 1. Les spécialistes pourraient recourir à l'algorithme quantique pour examiner des nœuds compliqués et recueillir ainsi des indices sur la véracité de la conjecture - ou trouver un contre-exemple.
Cela me rend confiant dans le fait que nous verrons des preuves intéressantes d'un avantage quantique dans un an ou deux
Le nouvel algorithme quantique pourrait également être utile en dehors des mathématiques. «En biologie, les nœuds sont intéressants», dit Meichanetzidis. Ce n'est pas spécialement le polynôme de Jones qui est important, mais des grandeurs comme la chiralité des macromolécules nouées, qui peuvent être calculées avec le polynôme. «Les macromolécules sont généralement si petites que les algorithmes classiques suffisent à les calculer. Mais s'il faut distinguer des nœuds avec des milliers d'intersections, alors il faut passer à un algorithme quantique.»
Dans leur travail, les chercheurs ont également pu déterminer à partir de quel point il est intéressant d'utiliser des algorithmes quantiques : selon les spécialistes, dès qu'il y a plus de 2800 croisements, un ordinateur quantique offre un avantage. L'ordinateur quantique actuel de Quantinuum, H2, ne peut pour l'instant examiner que des nœuds comportant une centaine d'intersections, mais l'ordinateur quantique Helios, actuellement en cours de développement et qui devrait être opérationnel à la mi-2025, pourrait atteindre l'avantage quantique pour la première fois. «S'ils parviennent à exécuter l'algorithme sur le prochain modèle quantique et à réellement surpasser les superordinateurs, ce serait l'un des premiers exemples deavantage quantique sur un problème qui n'a pas été inventé uniquement pour être exécuté sur des ordinateurs quantiques», a déclaré le physicien Aleks Kissinger de l'Université d'Oxford, qui n'a pas participé au travail,
au New Scientist.
«Cela me rend confiant dans le fait que nous verrons des preuves intéressantes d'un avantage quantique dans un an ou deux.»
Spektrum der Wissenschaft
Nous sommes partenaires de Spectre des Sciences et souhaitons vous rendre les informations fondées plus accessibles. Suivez Spectre des Sciences si vous aimez ses articles.
Originalartikel auf Spektrum.de
Des experts de la science et de la recherche rendent compte des dernières découvertes dans leur domaine – de manière compétente, authentique et compréhensible.