
Un carreau vampire prend la relève d'"Einstein
Un seul carreau, à partir duquel il est seulement possible de créer des motifs non périodiques : En mars 2023, le carreau Einstein a fait la une des journaux. Mais aujourd'hui, il existe un nouveau carreau aux formes encore plus raffinées, qui peut également se passer de reflets.
En mars 2023, une découverte mathématique a fait la une des journaux, même en dehors des milieux spécialisés : New York Times, CNN, Süddeutsche Zeitung et d'autres ont parlé de la forme géométrique de 13 pages qui rappelle à certains un chapeau et à d'autres un T-shirt. Ce polygone permet de couvrir un plan sans laisser d'espace - et le motif qui en résulte n'est toujours pas périodique.
Une forme qui répond à ces deux exigences est appelée carreau d'Einstein (le nom vient de "une pierre" et n'a rien à voir avec le célèbre physicien). Les mathématiciens en cherchaient une depuis des décennies, et certains avaient déjà abandonné tout espoir d'en trouver une. "Ce qui m'a le plus surpris, c'est la simplicité de la forme", explique le mathématicien Michaël Rao, de l'École normale supérieure de Lyon.
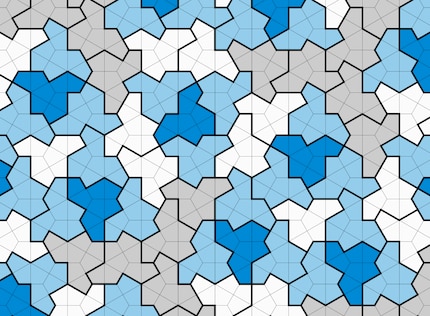
Source : D. Smith et al.
La tuile chapeau présentée au printemps 2023 présentait toutefois un bémol : pour qu'elle remplisse le plan sans laisser de vide, il fallait autoriser les reflets du treize-angle. "La grande question était de savoir s'il existait aussi un carreau d'Einstein qui ne nécessitait pas de réflexion", explique Rao. Certains appellent une telle forme le "carreau vampire", car, comme le personnage mythique de la nuit, il ne possède pas de reflet. Les découvreurs de la tuile chapeau, David Smith, Joseph Samuel Myers, Craig S. Kaplan et Chaim Goodman-Strauss, ont présenté une telle tuile vampire dans un travail non encore évalué sur la plateforme de prépublication ArXiv.
C'est encore un mathématicien amateur qui trouve la tuile vampire
Comme l'équipe l'a constaté dans sa première publication, il est possible de trouver d'autres formes de carreaux en modifiant la longueur des arêtes du chapeau, ce qui permet également de créer des pavages sans faille. Alors qu'il avait découpé l'une de ces formes de carreaux dans du papier et qu'il s'amusait à la manipuler, David Smith, technicien retraité des systèmes d'impression, a remarqué quelque chose de passionnant : Lorsqu'il assemblait les carreaux sans les faire se refléter, un motif sans faille et non périodique semblait apparaître.
"Naturellement, (Joseph Samuel Myers, Chaim Goodman-Strauss et moi-même) avons commencé à nous intéresser de plus près à cette forme", écrit l'informaticien Kaplan sur Mastodon. Après quelques mois de travail, lui et ses deux collègues ont pu prouver leurs soupçons : La tuile étudiée par Smith permet simplement des tuiles non périodiques si l'on n'autorise pas les parties en miroir.
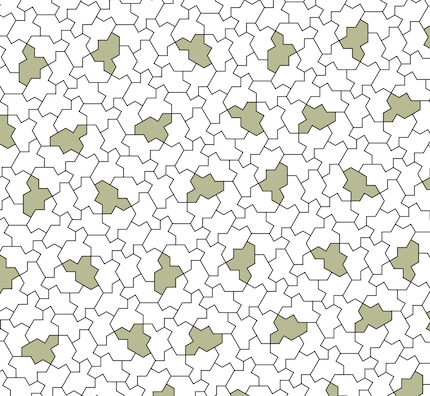
Source : David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss
Mais les scientifiques n'étaient pas entièrement satisfaits. En effet, si l'on insère des versions en miroir de la nouvelle tuile, il est possible de créer des motifs périodiques. C'est pourquoi ils ont modifié la forme du 13-angle et arrondi les coins, créant ainsi un nouveau carreau qui ressemble davantage à une pièce de puzzle. Cette tuile, qu'ils appellent "Spectre", ne peut recouvrir un calque sans laisser de vide que si l'on n'autorise pas les versions en miroir. Et, par la force des choses, les motifs créés ne sont pas périodiques. Les chercheurs affirment avoir ainsi trouvé un carreau de vampire : un Einstein cohérent qui n'a pas besoin de reflet pour paver un plan sans faille et forcément non périodique.
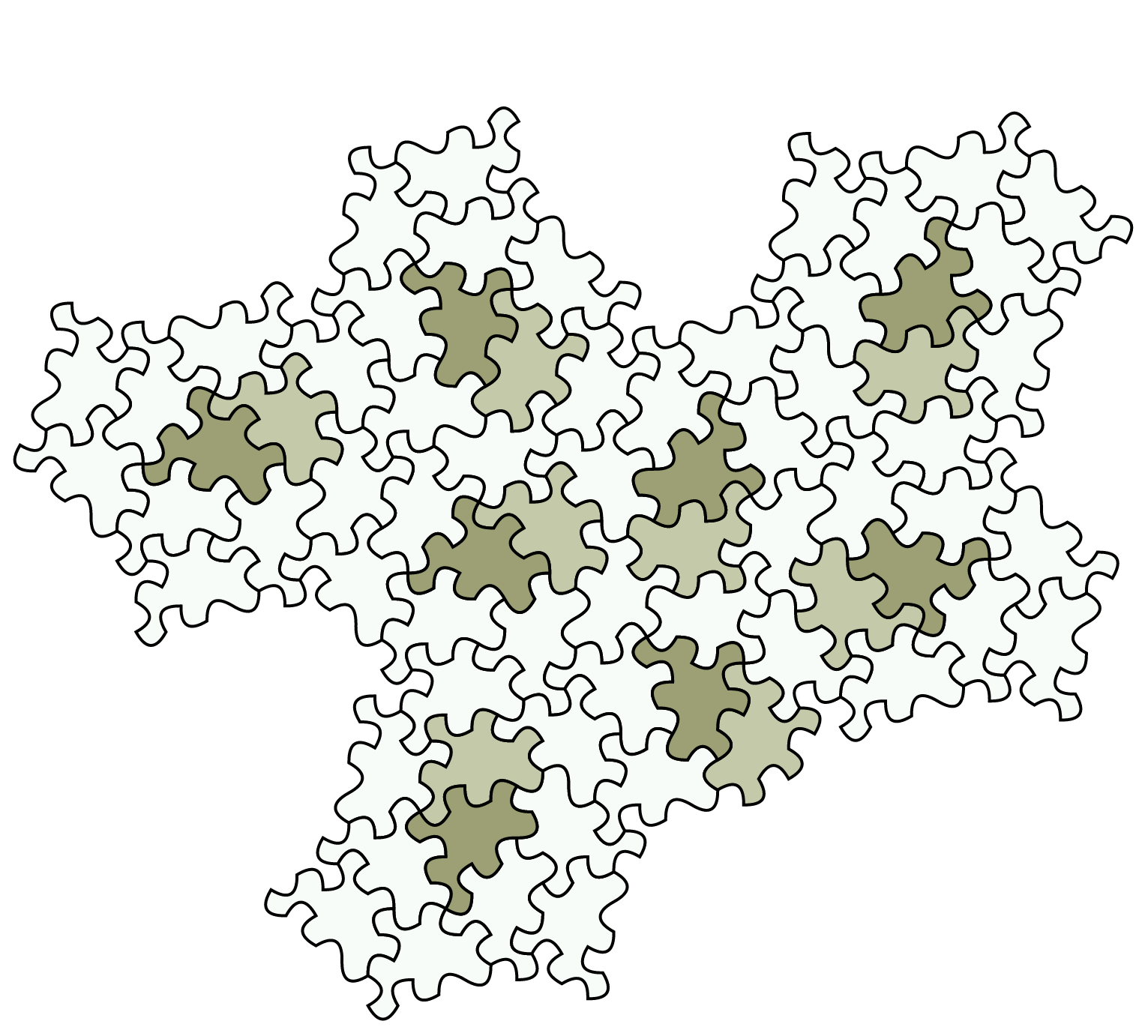
Source : David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss
Car certains spécialistes n'étaient pas satisfaits de la nécessité de mettre en miroir la tuile chapeau présentée en mars 2023. "Le problème n'est pas seulement qu'elle apparaisse en miroir", explique le mathématicien Michael Baake de l'université de Bielefeld, "mais que l'une des deux versions - en miroir ou non - apparaît nécessairement plus souvent que l'autre dans un carreau". Ce problème est lié à une propriété particulière des motifs apériodiques : Celui qui se trouve sur un plan carrelé de manière apériodique ne peut pas juger, à partir du motif, dans quelle zone du plan il se trouve ou de quel type de carrelage il s'agit - à partir d'un Einstein, on peut créer une infinité de carrelages différents. Mais comme il existe des parquets en chapeau avec des carreaux principalement réfléchis ou non réfléchis, on peut au moins faire la différence entre ces deux variantes. Mais cela va à l'encontre de la caractéristique même des parquetages apériodiques, qui ne permettent pas du tout de faire des distinctions.
En revanche, la tuile Spectre récemment découverte semble répondre à toutes les exigences d'une Einstein : Il s'agit d'un carreau unique et cohérent qui ne fait que tourner et se déplacer le long du plan, créant ainsi un motif sans faille et toujours irrégulier. Et comme il n'y a pas de reflet, il est également plus facile pour les fabricants de carrelage de produire les carreaux pour une salle de bain nerd parfaite.
Les mathématiciens ne peuvent toutefois pas encore se reposer sur leurs lauriers. "Il serait intéressant de découvrir de combien de pages au moins un carreau d'Einstein a besoin", explique Rao. "Ou si une tuile purement apériodique peut aussi être un polygone". Le nouvel objectif est donc de trouver une tuile d'Einstein aussi simple que possible. La chasse est ouverte.
Spektrum der Wissenschaft
Nous sommes partenaires de Spectre des Sciences et souhaitons vous rendre les informations fondées plus accessibles. Suivez Spectre des Sciences si vous aimez ses articles.
[[small:]]
Photo de couverture : David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss
Des experts de la science et de la recherche rendent compte des dernières découvertes dans leur domaine – de manière compétente, authentique et compréhensible.
Du nouvel iPhone à la résurrection de la mode des années 80. La rédaction fait le tri.
Tout afficher