Quel est le bon résultat ?
6 ÷ 2 (1+2) =
- 9 - est logique après tout50%
- 1 - vous êtes tous stupides ????!!!46%
- Je m'en fiche, les maths sont stupides de toute façon.5%
Le concours est terminé.
Quand Internet se dispute à propos des maths et que les calculettes sont en désaccord
24/5/2019
Traduction: traduction automatique
Des gens qui s'engueulent en ligne pour le moindre gugusse, ce n'est pas nouveau. En revanche, le fait qu'une discussion sur un problème mathématique génère des milliers de commentaires l'est. Les gens ne sont pas les seuls à obtenir des résultats différents, les calculatrices aussi. Quelle en est la raison ?
Un problème mathématique hante l'Internet depuis 2011. Depuis si longtemps, les gens se disputent sur les forums et tout le monde sait mieux. Actuellement, le problème d'une équation mathématique se retrouve à nouveau sur différentes plateformes en ligne. Dans un fil de discussion sur Facebook, plus de 1000 personnes se sont donné la réplique à cause des maths.
Le corpus delicti sur la page Facebook Word Porn:
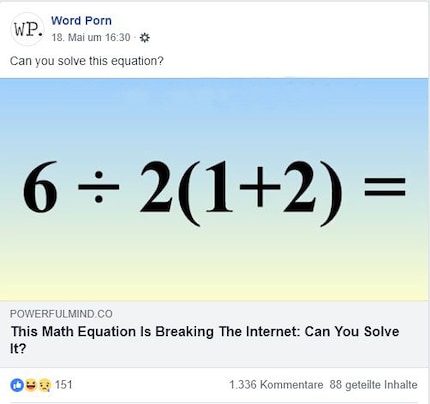
L'équation 6÷2(1+2) semble à première vue très simple. Elle implique une division, une multiplication et une addition entre parenthèses. La parenthèse est résolue et le résultat de la parenthèse est multiplié. C'est ainsi que nous l'avons tous appris à l'école primaire. En fait, c'est le cas. Car ce n'est pas si simple que ça.
Alors que certains disent que le résultat est 9, d'autres sont sûrs que l'équation donne 1.
Le problème
En fait, une équation simple comme celle-ci n'a qu'un seul résultat. Mais ici, cela peut être discuté. Le problème est la notation, qui donne un résultat différent selon les règles de notation appliquées. Ce qui est clair, c'est que l'équation peut être réécrite comme suit :
6÷2(1+2)=6÷2(3)
Le terme entre parenthèses doit d'abord être calculé.
Mais ensuite, on peut continuer à réécrire l'équation de deux manières différentes : Soit (6÷2)×3=9, soit 6÷(2×3)=1
.
Dans la première équation, on effectue d'abord la division, dans la seconde, on effectue d'abord la multiplication. La plupart des gens - et la plupart des calculatrices - résolvent l'équation de gauche à droite. Cela donne la solution 9, mais il existe certaines règles de notation qui, appliquées, rendent cette solution erronée. Le processus d'application des règles de notation s'appelle l'analyse syntaxique. Un parseur interprète, pour simplifier, une chaîne de caractères.
La règle de la multiplication implicite
La notation de l'équation est ambiguë. Elle est soit
(6÷2)×3=9 ou 6÷(2×3)=1. Il existe deux interprétations selon lesquelles la seconde notation, c'est-à-dire le résultat 1, est correcte. La première se base sur la multiplication implicite et explicite.
Dans certains manuels, la multiplication implicite a la priorité :
Par multiplication implicite, on entend en mathématiques la notation 2(1+2), c'est-à-dire la notation exprimée sans opérateur. Une multiplication explicite serait la notation 2×(1+2).
Cela signifie qu'il faut calculer 6÷(2×3)=1. Donc, si cette règle d'analyse syntaxique est appliquée, le résultat est 1. Mais cette règle n'est présente que dans certains manuels d'algèbre et non dans tous.
Pourquoi les calculatrices sont-elles en désaccord
?
Certaines calculatrices appliquent également cette règle lors de l'analyse syntaxique - c'est-à-dire l'interprétation - de l'équation. D'autres ne le font pas. Même les calculatrices du même fabricant calculent différemment.
Ce n'est toutefois pas la marque Casio qui est en cause. Les calculatrices de Texas Instruments n'arrivent pas non plus au même résultat. Les modèles TI-80, TI-81, TI-82 et TI-85 sont programmés pour donner la priorité à la multiplication implicite. Par contre, les modèles TI-83, TI-84 Plus, TI-89, TI-92 ne le sont pas, avec eux vous arrivez au résultat 9.
Un deuxième problème : des signes de division différents
Les interprétations de la multiplication implicite et explicite ne règlent malheureusement pas le problème. En effet, une division peut être représentée avec des notations différentes. Il y a l'obèle ÷ et la barre oblique /. Dans le passé, la division notée ÷ était traitée différemment de celle notée /. Au lieu d'évaluer les divisions et les multiplications de gauche à droite, ÷ indiquerait que tout ce qui est à gauche devrait être divisé par tout ce qui est à droite. Vous pouvez aussi vous représenter cela comme si vous notiez tout sur une barre de fraction.
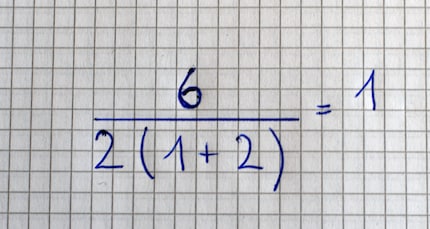
Avec l'obélisque, c'est-à-dire tel que l'équation est posée dans les forums, le résultat serait aussi à nouveau 1. Mais aucune des règles ci-dessus n'est largement répandue ni même généralement acceptée.
La solution
. Internet risque de se disputer encore longtemps sur la solution correcte. Pourtant, seule une personne se trompe. Il s'agit de la personne qui a formulé l'équation. Pourquoi cela ?
Le but d'une notation mathématique est d'être unique, de sorte que tout le monde l'interprète de la même manière, ce qui n'est clairement pas le cas ici. L'équation devrait être accompagnée d'une sorte de mode d'emploi
.
Faire des expériences et découvrir de nouvelles choses font partie de mes passions. Tout ne fonctionne pas toujours comme prévu et il arrive quelquefois que quelque chose se casse. Sinon, je suis accro aux séries et je ne peux plus me passer de Netflix. En été, on me trouve le plus souvent dehors au soleil – au bord du lac ou à un festival de musique.
65 commentaires
later