
La tessera Vampiro sostituisce la tessera "Einstein".
Una singola piastrella da cui è possibile creare solo modelli non periodici: La piastrella Einstein ha fatto notizia nel marzo 2023. Ma ora c'è una nuova mattonella, dalla forma ancora più ingegnosa, che riesce anche a non avere riflessi.
Nel marzo 2023, una scoperta matematica ha fatto notizia anche al di fuori del mondo specialistico: New York Times, CNN, Süddeutsche Zeitung e altri hanno parlato della forma geometrica a 13 lati, che ad alcuni ricorda un cappello e ad altri una maglietta. Questo poligono può essere utilizzato per coprire un piano senza spazi vuoti - e il modello risultante è sempre non periodico.
Una forma che soddisfa questi due requisiti è nota come piastrella di Einstein (il nome deriva da "pietra" e non ha nulla a che fare con il famoso fisico). I matematici erano alla ricerca di una mattonella di questo tipo da decenni e alcuni avevano già perso le speranze di trovarne una. "Sono rimasto particolarmente sorpreso dalla semplicità della forma", afferma il matematico Michaël Rao dell'École normale superieure di Lione.
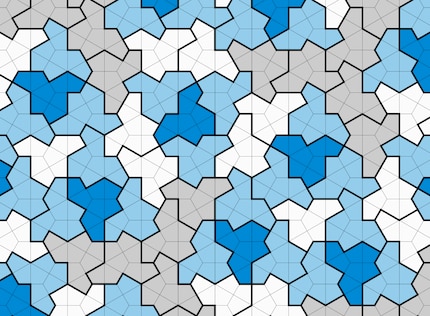
Fonte: D. Smith et al.
La mattonella a cappello presentata nella primavera del 2023 aveva però un inconveniente: per poter riempire il piano senza spazi vuoti, era necessario consentire le riflessioni dell'angolo 13. "La domanda principale era se esistesse una mattonella di Einstein che non avesse bisogno di essere riflessa", spiega Rao. Alcuni chiamano questa forma "mattonella vampiro" perché, come la mitica creatura notturna, non ha un'immagine speculare. Gli scopritori della mattonella cappello, David Smith, Joseph Samuel Myers, Craig S. Kaplan e Chaim Goodman-Strauss, hanno ora presentato tale mattonella vampiro in un articolo ancora non revisionato sulla piattaforma di preprint ArXiv.
Ancora una volta, è un matematico dilettante a trovare la mattonella vampiro
Come il team ha scoperto nella sua precedente pubblicazione, cambiando la lunghezza dei bordi del cappello, si possono trovare altre forme di piastrelle che creano pavimentazioni senza spazi vuoti. Quando David Smith, tecnico della tipografia in pensione, ha ritagliato una di queste forme di piastrelle dalla carta e ci ha giocato, ha notato qualcosa di interessante: Quando mise insieme le piastrelle senza specchiarle, sembrò emergere un disegno non periodico e privo di spazi.
"Naturalmente, (Joseph Samuel Myers, Chaim Goodman-Strauss e io) cominciammo a lavorare più intensamente su questa forma", scrive l'informatico Kaplan su Mastodon. Dopo alcuni mesi di lavoro, lui e i suoi due colleghi sono riusciti a dimostrare i loro sospetti: La piastrellatura studiata da Smith non permette semplicemente una piastrellatura periodica se non si ammettono parti speculari.
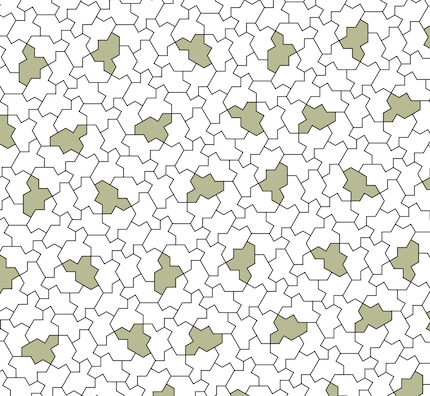
Fonte: David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss
Tuttavia, gli scienziati non erano del tutto soddisfatti. Dopo tutto, se si inseriscono versioni speculari della nuova mattonella, si possono generare modelli periodici. Per questo motivo hanno cambiato la forma della piastrella a 13 lati e hanno arrotondato gli angoli per creare una nuova piastrella che assomiglia più a un pezzo di puzzle. Questa tessera, che hanno chiamato "Spectre", può coprire un piano senza spazi vuoti solo se non sono ammesse versioni speculari. E i modelli generati non sono inevitabilmente periodici. Secondo i ricercatori, hanno quindi trovato una piastrella vampiro: un Einstein coerente che non ha bisogno di un'immagine speculare per ricoprire un piano senza spazi vuoti e necessariamente non periodico.
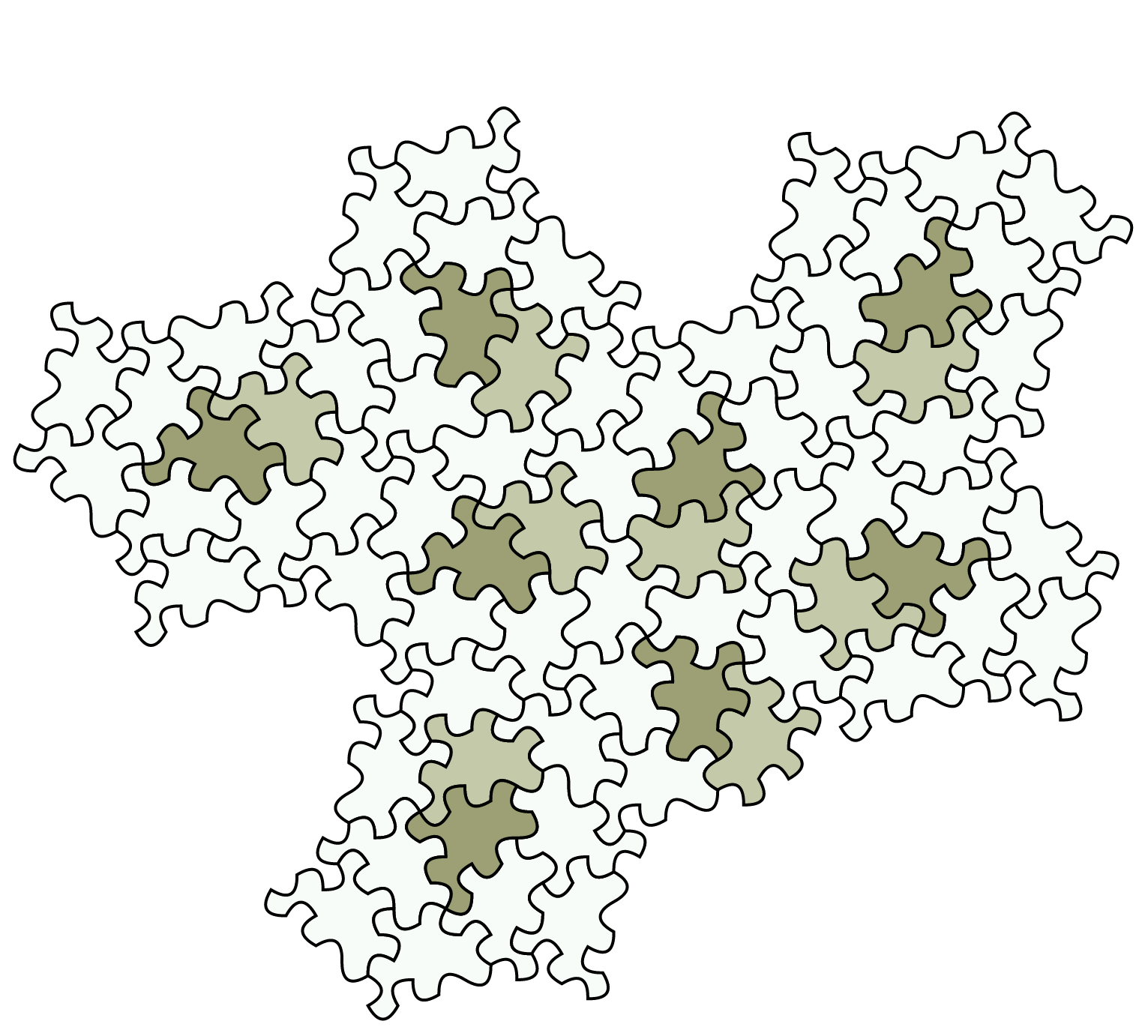
Fonte: David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss
Perché alcuni esperti non hanno gradito il fatto che la mattonella del cappello presentata nel marzo 2023 debba essere specchiata. "Il problema non è solo il fatto che appaia specchiata", afferma il matematico Michael Baake dell'Università di Bielefeld, "ma che una delle due versioni - specchiata o non specchiata - appare inevitabilmente più frequentemente in una piastrellatura rispetto all'altra": Chiunque si trovi su un piano piastrellato in modo aperiodico non può giudicare dal disegno in quale area del piano si trova o di che tipo di piastrellatura si tratta: da un Einstein si possono creare infiniti modelli di piastrellatura diversi. Tuttavia, poiché esistono modelli di parquet con piastrelle prevalentemente a specchio o prevalentemente non a specchio, è possibile distinguere tra queste due varianti. Tuttavia, ciò contraddice l'effettiva caratteristica del parquet aperiodico, che non consente alcuna differenziazione.
La nuova scoperta Spectre è un'altra cosa.
La piastrella Spectre appena scoperta, invece, sembra soddisfare tutti i requisiti di un Einstein: Si tratta di un'unica piastrella continua che viene semplicemente ruotata e spostata lungo il piano, creando un disegno senza spazi e sempre irregolare. E poiché non richiede alcuna specchiatura, è anche più facile per i produttori di piastrelle produrre le piastrelle per un perfetto bagno da nerd.
Ma i matematici non sono d'accordo.
Ma i matematici non possono ancora dormire sugli allori. "Sarebbe interessante scoprire di quanti lati ha bisogno una piastrella di Einstein come minimo", dice Rao. "Il nuovo obiettivo è quindi quello di trovare la mattonella di Einstein più semplice possibile". La caccia è aperta.
Spettro della scienza
Siamo partner di Spektrum der Wissenschaft e vogliamo rendere le informazioni fondate più accessibili a te. Segui Spektrum der Wissenschaft se ti piacciono gli articoli.
[[small:]]
Foto di copertina: David Smith, Joseph Samuel Myers, Craig S. Kaplan, Chaim Goodman-Strauss
Gli esperti della scienza e della ricerca riferiscono sulle ultime scoperte nei loro campi – competenti, autentiche e comprensibili.
Dal nuovo iPhone al revival della moda anni '80. La redazione fa chiarezza.
Visualizza tutti