
A quantum computer analyses mathematical knots
It is extremely difficult to distinguish knots from one another. A new quantum algorithm could help mathematicians with this mammoth task in the future.
Can you tell the difference between a bowstring loop and a boatswain's knot at first glance? No? You're probably not alone. Even for scientists, this type of problem is not trivial. In fact, one of the most important tasks of topology is to find reliable methods to distinguish different knots from one another. This is because they not only play an important role in mathematics: nodes also occur time and again in physics and biology.
Mathematicians have therefore introduced so-called invariants: characteristic quantities that differ from node to node. The Jones polynomial, introduced in 1984, has proven to be particularly helpful. Identical knots always have the same Jones polynomial. The problem: for complicated knots, it is very time-consuming to determine the associated polynomial - or even to calculate it for certain values. However, researchers led by physicist Konstantinos Meichanetzidis have now developed a quantum algorithm that efficiently analyses Jones polynomials - even when conventional computers fail at the task. They have presented their results in a paper that has not yet been peer-reviewed.
Knots have accompanied mankind for thousands of years. However, mathematicians have only been studying them since the 19th century. Mathematical knots differ slightly from what we understand them to be in everyday life: in mathematics, knots are always closed, as if the ends of a shoelace were glued together. For their investigations, the experts began to draw them. Knots are actually curves in three-dimensional space, but they projected the shapes onto a plane, which makes it easier to work with them. However, the question soon arose: when do two images correspond to one and the same knot?
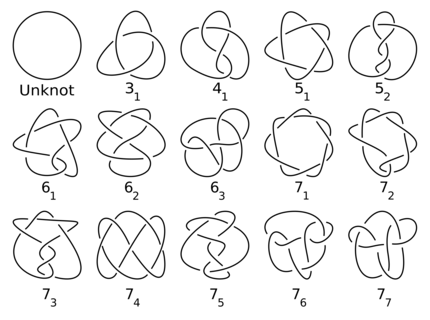
Source: jkasd / Knoten-Tabelle
Simple nodes are still quite easy to distinguish, but it is difficult to keep track of specimens with many crossings. In these cases, the Jones polynomial helps. The intersections can be used to assign a polynomial to a node that fulfils the following properties: Two identical nodes have the same polynomial, while a non-node has the polynomial 1.
This is super interesting - and a rather strange connection between maths and quantum computation
However, the definition of the Jones polynomial does not rule out the possibility of two different nodes having the same polynomial (although this rarely happens). Nevertheless, the Jones polynomial proves to be extremely useful - especially as it is related to quantum physics and thus unexpectedly connects knot theory with a completely different field of research. «This is super interesting - and a rather strange connection between maths and quantum computation», says Meichanetzidis, lead author of the current quantinuum study.
In principle, the Jones polynomial of a knot can always be calculated - but as the complexity of the knot increases, the task becomes extremely tedious. In fact, the number of calculation steps required to calculate the polynomial increases exponentially with the number of intersections of a node. Conventional computers are therefore quickly at a loss when the nodes become too complicated. Even quantum computers can't help: unfortunately, known quantum algorithms cannot prevent the number of calculation steps from increasing exponentially.
On the way to a useful quantum advantage
But quantum computers offer another advantage: As early as 2005, physicists led by computer scientist Dorit Aharonov showed that quantum computers could efficiently approximate the Jones polynomial of a node for certain values - i.e. the number of computing steps required only grows polynomially with the number of crossings. Researchers at the quantum computer company Quantinuum have now developed and implemented such a quantum algorithm in detail. An ordinary computer, on the other hand, still requires an extremely large number of calculation steps even for this approximation, the number of which grows exponentially with the size of the node.
«If we evaluate our quantum algorithm for different values, we can use it to efficiently differentiate between nodes with a high probability», explains Meichanetzidis. For example, if several analyses of the Jones polynomial produce the same result for two nodes, then it is likely that both nodes are the same. This can be utilised within the framework of knot theory, for example to address some of the open conjectures in the field. For example, the Jones conjecture states that apart from the non-node, no node has a Jones polynomial of 1. Experts could resort to the quantum algorithm to investigate complicated knots and thus gather evidence for the correctness of the conjecture - or find a counterexample.
This makes me confident that we will see interesting evidence of a quantum advantage in a year or two
The new quantum algorithm could also be useful outside of maths. «In biology, knots are of interest», says Meichanetzidis. It is not specifically the Jones polynomial that is important here, but quantities such as the chirality of knotted macromolecules, which can be calculated using the polynomial. «The macromolecules are usually so small that classical algorithms are sufficient to calculate them. But if you have to differentiate between nodes with thousands of crossings, then you should switch to a quantum algorithm.»
In their work, the researchers were also able to determine the point at which the use of quantum algorithms is worthwhile: according to the experts, a quantum computer offers an advantage as soon as there are more than 2800 intersections. Quantinuum's current quantum computer, H2, can currently only analyse nodes with around 100 intersections, but the Helios quantum computer, which is currently under development and should be ready for use in mid-2025, could achieve the quantum advantage for the first time. «If they can run the algorithm on the next quantum model and truly outperform supercomputers, this would be one of the first examples of a quantum advantage in a quantum computer.r a quantum advantage on a problem that wasn't just invented to run on quantum computers», said physicist Aleks Kissinger of the University of Oxford, who was not involved in the work,
told the New Scientist.
«This gives me confidence that we will see interesting evidence of a quantum advantage in a year or two.»
Spectrum of Science
We are a partner of Spektrum der Wissenschaft and want to make sound information more accessible to you. Follow Spektrum der Wissenschaft if you like the articles
Originalartikel auf Spektrum.de
Experts from science and research report on the latest findings in their fields – competent, authentic and comprehensible.
From the latest iPhone to the return of 80s fashion. The editorial team will help you make sense of it all.
Show all