
Un computer quantistico analizza i nodi matematici
È estremamente difficile distinguere i nodi gli uni dagli altri. Un nuovo algoritmo quantistico potrebbe aiutare i matematici a svolgere questo compito immane in futuro.
Riesci a capire la differenza tra un passante per l'arco e un nodo del nostromo a prima vista? No? Probabilmente non sei il solo. Anche per gli scienziati questo tipo di problema non è banale. Infatti, uno dei compiti più importanti della topologia è quello di trovare metodi affidabili per distinguere i diversi nodi l'uno dall'altro. Questo perché i nodi non giocano un ruolo importante solo in matematica: i nodi sono presenti anche in fisica e in biologia.
I matematici hanno quindi introdotto i cosiddetti invarianti: quantità caratteristiche che differiscono da nodo a nodo. Il polinomio di Jones, introdotto nel 1984, si è rivelato particolarmente utile. Nodi identici hanno sempre lo stesso polinomio di Jones. Il problema: per i nodi complicati, determinare il polinomio associato - o addirittura calcolarlo per determinati valori - richiede molto tempo. Tuttavia, i ricercatori guidati dal fisico Konstantinos Meichanetzidis hanno ora sviluppato un algoritmo quantistico che analizza in modo efficiente i polinomi di Jones, anche quando i computer convenzionali falliscono in questo compito. Hanno presentato i loro risultati in un articolo che non è ancora stato sottoposto a peer-review.
I nodi accompagnano l'umanità da migliaia di anni. Tuttavia, i matematici li studiano solo dal XIX secolo. I nodi matematici differiscono leggermente da come li intendiamo nella vita di tutti i giorni: in matematica, i nodi sono sempre chiusi, come se le estremità di un laccio fossero incollate tra loro. Per le loro indagini, gli esperti iniziarono a disegnarli. I nodi sono in realtà curve nello spazio tridimensionale, ma hanno proiettato le forme su un piano, il che rende più facile lavorare con loro. Tuttavia, è subito sorta una domanda: quando due immagini corrispondono a uno stesso nodo?
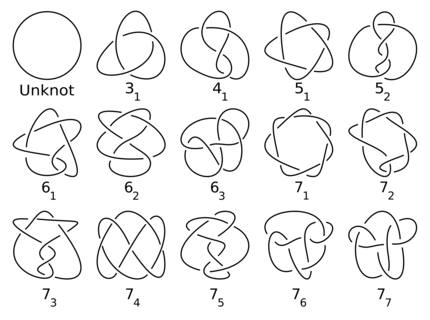
Fonte: jkasd / Knoten-Tabelle
I nodi semplici sono ancora abbastanza facili da distinguere, ma è difficile tenere traccia degli esemplari con molti incroci. In questi casi, il polinomio di Jones ci aiuta. Le intersezioni possono essere utilizzate per assegnare un polinomio a un nodo che soddisfa le seguenti proprietà: Due nodi identici hanno lo stesso polinomio, mentre un non nodo ha il polinomio 1.
Questo è super interessante - e una connessione piuttosto strana tra matematica e calcolo quantistico
Tuttavia, la definizione del polinomio di Jones non esclude la possibilità che due nodi diversi abbiano lo stesso polinomio (anche se questo accade raramente). Tuttavia, il polinomio di Jones si rivela estremamente utile, soprattutto perché è legato alla fisica quantistica e quindi collega inaspettatamente la teoria dei nodi con un campo di ricerca completamente diverso. «Si tratta di una connessione molto interessante e piuttosto strana tra la matematica e la computazione quantistica», afferma Meichanetzidis, autore principale dell'attuale studio sul quantinuum.
In linea di principio, il polinomio di Jones si dimostra estremamente utile, soprattutto perché è legato alla fisica quantistica e quindi collega la teoria dei nodi a un campo di ricerca completamente diverso.
In linea di principio, il polinomio di Jones di un nodo può sempre essere calcolato, ma con l'aumentare della complessità del nodo, il compito diventa estremamente noioso. Infatti, il numero di passaggi necessari per calcolare il polinomio aumenta esponenzialmente con il numero di intersezioni di un nodo. I computer convenzionali si trovano quindi rapidamente in difficoltà quando i nodi diventano troppo complicati. Nemmeno i computer quantistici possono essere d'aiuto: purtroppo gli algoritmi quantistici conosciuti non possono evitare che il numero di passaggi di calcolo aumenti esponenzialmente.
Sulla strada di un utile vantaggio quantistico
Ma i computer quantistici offrono un altro vantaggio: Già nel 2005, i fisici guidati dall'informatico Dorit Aharonov hanno dimostrato che i computer quantistici possono approssimare in modo efficiente il polinomio di Jones di un nodo per determinati valori, ovvero il numero di passi di calcolo necessari cresce solo polinomialmente con il numero di incroci. I ricercatori dell'azienda di computer quantistici Quantinuum hanno ora sviluppato e implementato in dettaglio un algoritmo quantistico di questo tipo. Un computer ordinario, invece, richiede un numero estremamente elevato di passaggi di calcolo anche per questa approssimazione, il cui numero cresce esponenzialmente con la dimensione del nodo.
«Se valutiamo il nostro algoritmo quantistico per valori diversi, possiamo usarlo per differenziare in modo efficiente i nodi con un'alta probabilità», spiega Meichanetzidis. Ad esempio, se diverse analisi del polinomio di Jones producono lo stesso risultato per due nodi, è probabile che entrambi i nodi siano uguali. Questo può essere utilizzato nell'ambito della teoria dei nodi, ad esempio per risolvere alcune delle congetture aperte in questo campo. Ad esempio, la congettura di Jones afferma che, a parte il non-nodo, nessun nodo ha un polinomio di Jones uguale a 1. Gli esperti potrebbero ricorrere all'algoritmo quantistico per studiare nodi complicati e raccogliere così prove della correttezza della congettura - o trovare un controesempio.
Questo mi rende fiducioso sul fatto che vedremo prove interessanti di un vantaggio quantistico tra un anno o due
Il nuovo algoritmo quantistico potrebbe essere utile anche al di fuori della matematica. «In biologia, i nodi sono interessanti», dice Meichanetzidis. Non è il polinomio di Jones a essere importante in questo caso, ma quantità come la chiralità delle macromolecole annodate, che possono essere calcolate utilizzando il polinomio. «Le macromolecole sono solitamente così piccole che gli algoritmi classici sono sufficienti per calcolarle. Ma se devi distinguere tra nodi con migliaia di incroci, allora dovresti passare a un algoritmo quantistico.»
Nel loro lavoro, i ricercatori sono riusciti anche a determinare il punto in cui vale la pena utilizzare gli algoritmi quantistici: secondo gli esperti, un computer quantistico offre un vantaggio non appena ci sono più di 2800 intersezioni. L'attuale computer quantistico di Quantinuum, H2, può attualmente analizzare solo nodi con circa 100 intersezioni, ma il computer quantistico Helios, attualmente in fase di sviluppo e che dovrebbe essere pronto per l'uso a metà del 2025, potrebbe raggiungere per la prima volta il vantaggio quantistico. «Se riuscissero a eseguire l'algoritmo sul prossimo modello quantistico e a superare davvero i supercomputer, questo sarebbe uno dei primi esempi di vantaggio quantistico in un computer quantistico.r un vantaggio quantistico su un problema che non è stato inventato solo per funzionare sui computer quantistici», ha detto il fisico Aleks Kissinger dell'Università di Oxford, che non ha partecipato al lavoro,
ha dichiarato al New Scientist.
«Questo mi dà fiducia nel fatto che vedremo prove interessanti di un vantaggio quantistico entro un anno o due.»
Spettro della Scienza
Siamo partner di Spektrum der Wissenschaft e vogliamo renderti più accessibile l'informazione scientifica. Segui Spektrum der Wissenschaft se ti piacciono gli articoli
Originalartikel auf Spektrum.de
Gli esperti della scienza e della ricerca riferiscono sulle ultime scoperte nei loro campi – competenti, autentiche e comprensibili.
Dal nuovo iPhone al revival della moda anni '80. La redazione fa chiarezza.
Visualizza tutti